■擎曄有限公司
前言
電腦斷層掃描(Computed Tomography, 簡稱 CT)正逐漸成為材料科學和材料開發領域的業界標準,特別是應用於纖維材料研究時,電腦斷層掃描可在不破壞樣本纖維特徵的前提下,多維度 / 多角度檢視材料纖維結構,並可結合原位實驗 (in-situ experiments)或數值模擬,進一步評估材料的物理特性。當前的主要挑戰在於如何在影像解析度與影像資料處理量之間取得折衷,以期獲得精確的纖維材料資訊。在這些統計數據中,本文裡將介紹材料影像處理分析軟體“Avizo”裡使用的三種在不同影像解析度下的分析方式,尤其著重材料中纖維分佈的排向追蹤討論,希冀提供適當的建議予不同的纖維材料分析運用。
方法介紹
在影像處理軟體 Avizo 裡,透過三種不同的方法,沿著影像的軸向,擷取預定的尺寸及選定的位置,來計算局部纖維排向:1.FFT,是基於傅立葉頻譜的主成分分析 [1]; 2. GRAD,則是基於局部梯度的分析 [2]。這兩種方法主要透過影像的紋理來計算纖維的局部排向,因此,即使在無法分辨單根纖維的低解析度影像數據,仍然能夠提供計算結果。而第三種方法“XFIBER”[3,4] 的演算基礎,主要是基於樣本圓柱的比對及其獨家的纖維追蹤演算法,可分離出每一根獨立的纖維,並計算每根纖維中心線,因此,所有纖維的參數,例如纖維數量、排向、長度、直徑與曲折度
等統計資料都可以透過 Avizo XFIBER 計算。以上提及的三種方法皆針對相同的局部影像數據進行分析,並計算生成張量,透過張量,來檢視局部體積中纖維排向。三種方法都會計算得到對稱張量,透過求解張量特徵值,分解出主要排向和分散排向的資訊。在 XFIBER 的方法中,因為每根獨立的纖維都已計算取得,纖維排向張量可精確地進行計算 [5]。其定義為每根纖維排向的單位向量之外部乘積,再乘上相應的纖維長度 (L) 加權:而 FFT 和 GRAD 則是從影像紋理來推算張量,從而使其運算的張量結果無法直接應用,因此三組數據較難直接進行比較。例如在 FFT 的計算,主要方向是對應於最小的高頻變化,因此求解特徵向量時,會對應於最低特徵值的特徵向量。相反的,GRAD 和 XFIBER,則是對應於最大特徵值的特徵向量。因此,本文是基於計算張量及主要排向的統計數據進行比較。
資料來源
產生影像數據
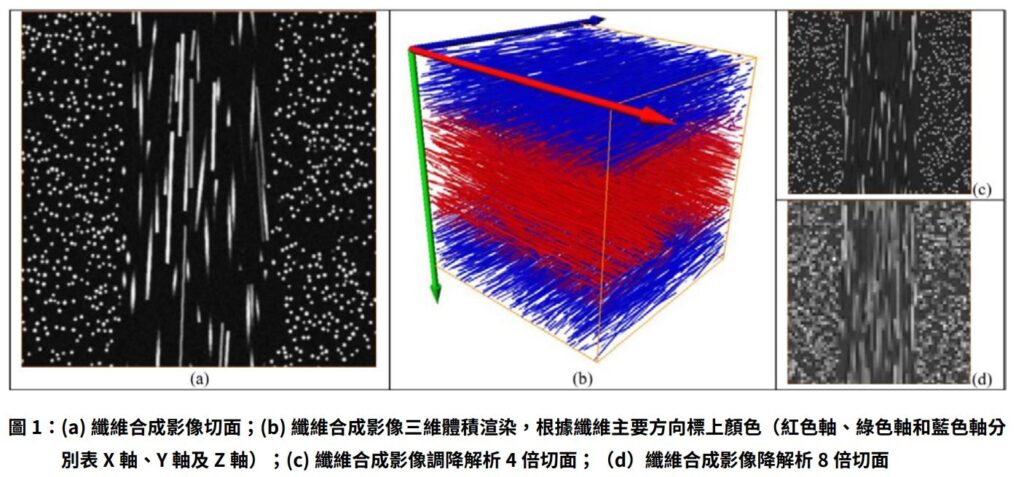
本文我們透過皮芯結構方式(skin-core structure),生成非重疊、直線的纖維影像,透過這組合成影像,比較三種方法在纖維定量分析的結果。合成影像中纖維的生成是使用 force-biased 演算法 [6],計算過程會依序隨機的在選定的區域,依照自訂的位置、長度、排向和直徑插入纖維,之後演算法會再將有重疊的纖維進行旋轉和位移微調,纖維直徑也會在計算過程中略為縮小,確認演算可以正確收斂,我們就可以得到一組纖維占比約 10% 的合成影像。合成影像最後會再經過一些離散處理,包含插入高斯雜訊及模糊化
等,並確保纖維直徑符合 5 個體像素,最後再將其轉換為 512x512x512 的影像,如圖 1 所示。
玻璃纖維複合材料
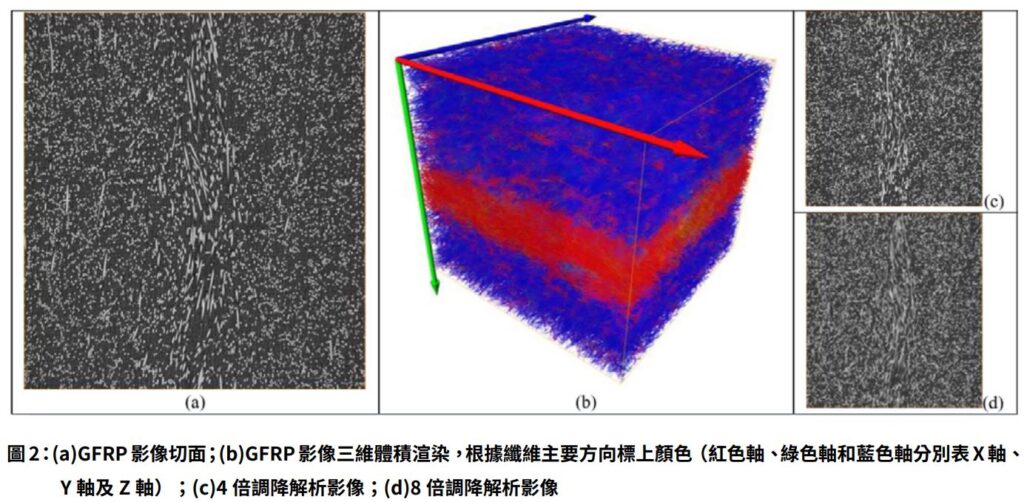
此外,我們也將這些方法針對實際玻璃纖維增強聚合物 (GFRP) 的微電腦斷層影像進行分析,如圖 2 所示。此聚合物中的纖維為平均直徑為 10μm 的標準短玻璃纖維,在選定的 2x2x2 立方公厘區域纖維的占比為17%,聚合物的大小約為 2x2x2mm³。掃描解析度為1.5μm,該解析足以區分單個纖維。
分析結果
三維影像會依軸向切分為若干立方區域,並用本文中的三種方法計算局部纖維排向。兩組影像數據都具備Skin-core 相似的正交纖維。大部份切分區域的纖維其主要方向為 X 軸向或 Z 軸向,少部份區域是混合纖維,而這些混合纖維主要是沿 X 軸或是 Z 軸。兩組影像資料會利用影像原始最高解析進行局部纖維排向的比較分析,同時,為能測試三種演算法的穩定度,使用 Lanczos 調降解析 4 倍後以及調降解析 8 倍後的影像,也會進行相同的纖維排向分析。
合成影像數據
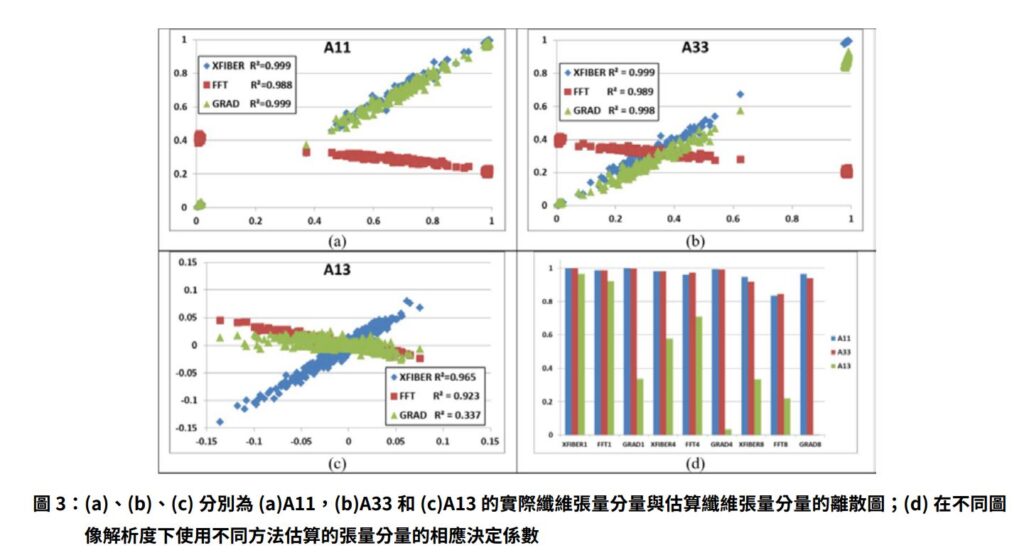
對 於 合 成 影 像, 我 們 使 用 上 述 與 XFIBER 相 同 的 方程式 (eq.1) 計算纖維參考張量作為比較的基準,與XFIBER 不同的是,該纖維是離散化運算之前的實際纖維數據,而 XFIBER 的運算則是針對生成的灰階影像,分離每根獨立的纖維後,再進行纖維張量計算。從整體分析數據,不同計算方式與纖維參考張量間有很高的統計關係,如圖 3 所示,幾乎是線性相關。除GRAD 方法中的對角線分量 A13 外,其餘決定係數 R2都非常高。從圖 3(d) 中,則可看出仍維持統計關係的趨勢,但對非對角分量的量測則會變得困難,且數據結果無法重複計算取得,不過因合成影像僅少數纖維的方向偏離兩個主要的方向,因此,我們無法在此進行結論。值得一提,儘管 XFIBER 方法在降低解析影像的分析結果,其纖維偵測的準確性明顯下滑,但在排向的測量統計數據顯示,仍有一定程度價值。
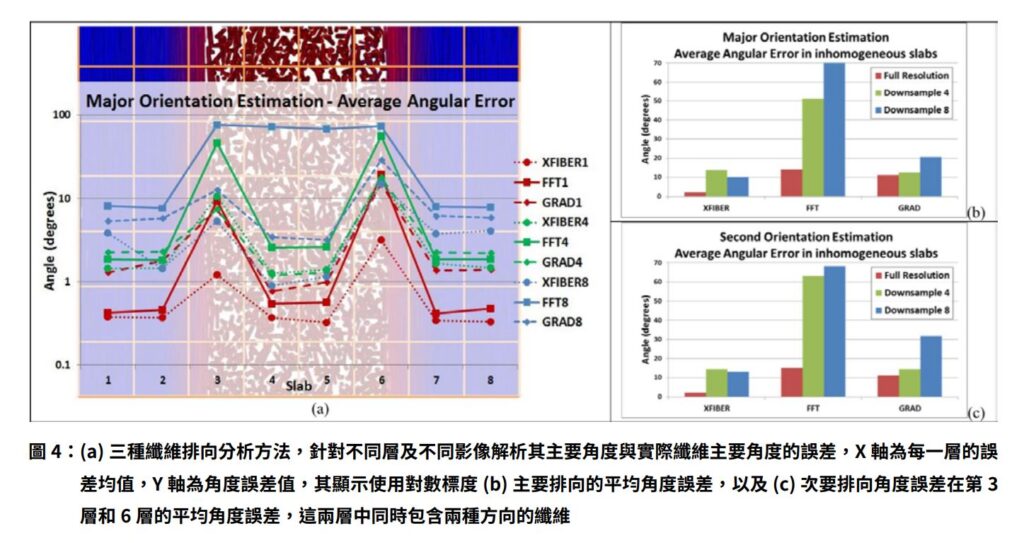
沿著層厚方向分層檢視數據,以獲得更精確的結果,在分層數據中,我們發現除了第 3 層及第 5 層外,其它層的纖維排向都是一致的,第 4 層和第 5 層纖維沿著 X 軸,第 1 層、第 2 層、第 7 層及第 8 層沿著 Z 軸,而第 3 層與第 6 層則包含混合 X 軸向與 Z 軸向的纖維,其中約有 2/3 纖維沿著 X 軸向,1/3 沿著 Z 軸向,影像可以參考圖 4(a)。
在相同排向層(除了第 3 層及第 6 層外),三種分析方法的平均角度誤差(真實纖維主要排向與計算排向的 夾 角 ) 都 非 常 低,XFIBER、FFT 和 GRAD 分 別 為0.35、0.48 和 1.26 度。另一方面,在混合排向層(第 3 層及第 6 層)中,基於紋理方法來計算纖維排向,已證明會有顯著的錯誤,而纖維追蹤的方法則依然非常精確。同時,在圖 4(b) 中,與基於紋理的量測方法的 GRAD,尤其是FFT 比較,XFIBER 在不同解析影像的分析結果還是明顯正確且穩定的。
玻璃纖維複合材料
我們也對玻璃纖維強化塑膠樣品進行了類似的研究分析,因無法預知纖維真實排向,我們使用 XFIBER 在最高解析影像的分析結果作為我們比較的參考,結果如圖 5 所示。與合成影像一樣,針對整體分析數據,不同方法的分析結果和參考張量有很強的相關性。張量的決定係數都非常高,在相同排向區,其主要排向角度誤差也在5 度以內,且在調降 8 倍解析後,其角度誤差仍然維持在 12 度內。
然而,在混合排向第 4 層和第 7 層,也就是纖維交錯的界面處,不同的方法就有顯著的差異,XFIBER 的方法估算的纖維排向在不同影像解析較為一致(主要與次要排向在調降 4 倍解析的角度差異小於 10 度),其它兩種方法纖維角度有較大的偏差(大約在 20 度或更大角度)。
結論
本文針對複合纖維材料微電腦斷層影像,以估算局部纖維排向及其統計數據的差異,做出 Avizo 內三種基於影像紋理量測及單根纖維追蹤分離技術的方法比較。運用這些方法,我們處理了皮芯玻璃纖維增強聚合物及另一組相似的人工合成纖維影像數據,由於人工合成纖維有已知的纖維材質訊息,遂可當作分析時參考的黃金標準。此外本文也探討各種方法在調降影像解析度的穩定性,提供參考資訊,因為在進行電腦斷層影像擷取時,究竟是要選擇較高的放大倍率來觀察較小的視野,還是選擇使用較低解析度但採集較大樣品區域常是很困難的決定。結果顯示無論在合成影像或真實影像,對張量估算纖維排向結果,在不同方法大致是一致的,在調降解析的影像分析結果,也相對合理。有趣的是,當影像解析達到纖維直徑時,纖維追蹤準確度與效能明顯下滑,但其用於分辨樣本排向的結果仍相當合理。
本文使用的纖維樣本結構,讓我們可以分析相同纖維排向區域,該區域的纖維全部具有相似的排列方向;及混合纖維排向區域,該區域的纖維互相交錯。在相同纖維排向的區域,儘管使用纖維追蹤的方法在較高解析的影像上有較精確的結果外,本文使用的方法基本上都還正確;然而在混合纖維區域,基於紋理特徵的演算法,其準確性就明顯降低,不過使用纖維追蹤的方式則依然正確,就算調降影像解析的分析結果,也有相同的現象。因此,在利用影像分析交錯或複雜方向分佈的纖維材料,例如編織纖維、模製複合材料或是更隨機分佈的纖維材料,就要留意分析的方法,以得到正確合理的分析結果。
参考文献
[1].Bigün et al. (1987). Optimal orientation detection of linear symmetry, in Proc. ICCV, pp. 433-438.
[2].Püspöki et al. (2016). Transforms and Operators for Directional Bioimage Analysis: A Sur vey. Advances in Anatomy,Embryology and Cell Biology, vol. 219(3): 69-93.
[3].Roseman (2003). Particle finding in electron micrographs using a fast local correlation algorithm. Ultramicroscopy, 94(3-4):225-236.
[4].Weber et al. (2012). Automated tracing of microtubules in electron tomograms of plastic embedded samples of caenorhabditis elegans embryos. Journal of Structural Biology, 178(2):129-138.
[5].Advani, Tucker (1987). The use of tensors to describe and predict fiber orientation in short fiber composites. Journal of Rheology, 31(8), 751.
[6].Bezrukov et al. (2006). Simulation and statistical analysis of random packings of ellipsoids. Particle & Particle Systems Characterization, 23(5), 388-398.